28. 01. 2021
Verfasst von: Yskert von Kodolitsch, Carl Rudolf Blankart, Thomas Wick
Interventionsmodell für Pandemien
Wie lässt sich in Krisenzeiten die Rationalität bei der Auswahl von Interventionsmaßnahmen verbessern? Anlässlich der Corona-Pandemie erarbeiten derzeit ein Mediziner, ein Ökonom und ein Mathematiker in einem Kooperationsprojekt ein Interventionsmodell. Es soll die Grundlagen für politische, ökonomische, gesellschaftliche sowie individuelle Entscheidungen liefern.
Grundlage für Strategie und Entscheidungen
Ursache und Wirkung sind für die Bevölkerung in Krisenzeiten nicht immer leicht auseinanderzuhalten. Ein mathematisches Modell analysiert die Auswirkungen der Covid-19-Erkrankungen, der durchgeführten Interventionen und der politischen Entscheidungen. Mit mathematischen Strukturen werden die medizinischen und ökonomischen Beobachtungen abgebildet und modelliert. „Dies legt die Ursache-Wirkungszusammenhänge sowohl auf gesellschaftlicher als auch auf individueller Ebene offen, woraufhin sich zielorientierte Entscheidungen formulieren lassen“, erklärt Prof. Thomas Wick von der Leibniz Universität Hannover.
Ökonomische und soziale Resilienz
Gemeinsam mit Prof. Yskert von Kodolitsch vom Universitätsklinikum Hamburg-Eppendorf sowie Prof. Carl Rudolf Blankart von der Universität Bern erstellt Thomas Wick ein neues Modell. Es verknüpft dabei Konzepte der Epidemiologie, der Resilienzforschung und der strategischen Entscheidungsfindung. Eine Hauptaufgabe bei der Modellerstellung ist es, Einflussfaktoren und deren Parametrisierungen zu spezifizieren. Als Beispiel nennt Thomas Wick die zeitliche Entwicklung der ökonomischen und sozialen Resilienz in Abhängigkeit der infizierten Personen. „Scheinbar stabile Systeme können einen Kipppunkt passieren und dann sehr plötzlich kollabieren“, veranschaulicht der Mathematiker. „Mathematisch sind dies sogenannte Nichtlinearitäten.“
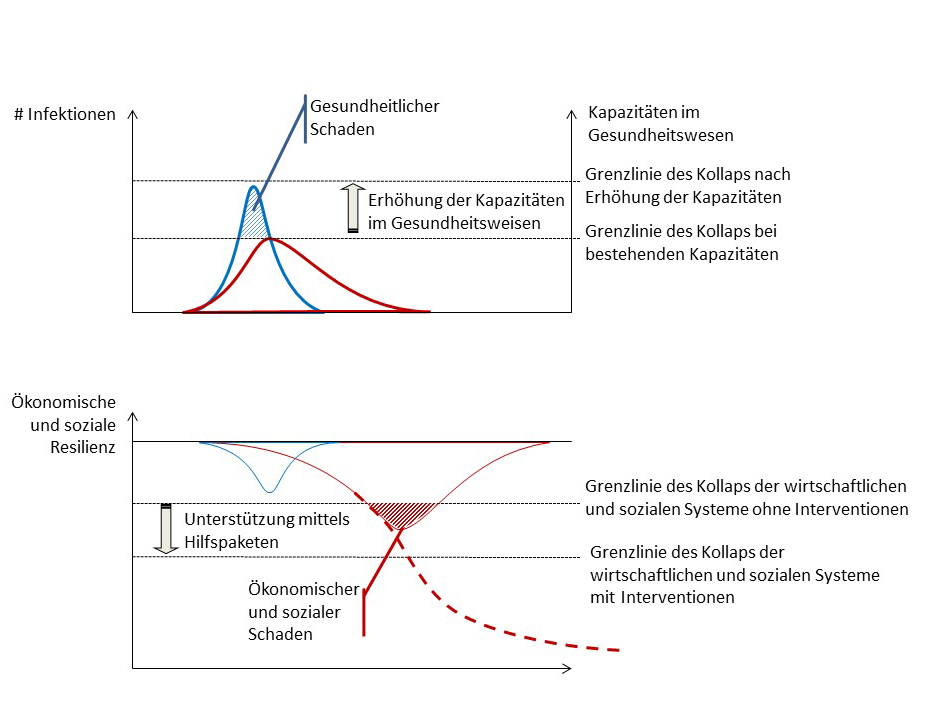
Mit Hilfe des grundlegenden Rahmenwerks lassen sich Effekte der Pandemie und der Interventionen systemübergreifend darstellen und diskutieren: Bleiben das öffentliche, private und berufliche Leben ohne Lockdown-Maßnahmen oder Kontaktsperren erhalten (blaue Kurven, siehe Abbildung), führt das zu einer Überlastung des Gesundheitssystems und letztlich zu dessen Kollaps. In diesem Szenario ist die Wirtschaft weniger stark betroffen. Mit Lockdown-Maßnahmen (rote Kurven) werden die Kapazitäten des Gesundheitssystems entlastet und ein Zusammenbruch wird vermieden. Hingegen ist die Wirtschaft stark betroffen und kollabiert.
Wendepunkt für Aufschwung erreichen
Eine Interventionsstrategie hat zum Ziel, die Grenzlinie des Kollapses zu verschieben. Mathematisch markiert sie damit einen Wendepunkt und ermöglicht so einen wirtschaftlich-sozialen Aufschwung. „Ein Einbruch im Gesundheitswesen oder im wirtschaftlich-sozialen Bereich lässt sich vermeiden, indem beispielsweise die Anzahl der Intensivbetten und des Personals im Gesundheitssektor erhöht wird“, führt Thomas Wick aus. „Im wirtschaftlich-sozialen Bereich können Stützungsmaßnahmen wie Kurzarbeit oder Überbrückungsgelder einen Zusammenbruch verhindern.“ Das Modell und der interdisziplinäre Ansatz bieten die Chance, auch bei der nächsten Pandemie strukturiert vorgehen zu können.
Hier finden Sie weitere Informationen:
Projektpartner:

Leibniz Universität Hannover

Leibniz Universität Hannover

30169 Hannover

30169 Hannover